

Principal Component Analysis (PCA) is one of the most fundamental algorithms for dimension reduction and is a foundation stone in Machine Learning. It has found use in a wide range of fields ranging from Neuroscience to Quantitative Finance with the most common application being Facial Recognition.
Some of the applications of Principal Component Analysis (PCA) are:
We will go through a basic introduction to PCA before going into each application in detail.
Principal Component Analysis (PCA) is a dimensionality reduction technique invented by Karl Pearson in 1901, which is used for identification of a smaller number of uncorrelated variables known as Principal Components from a larger set of data. The figure below illustrates the same:
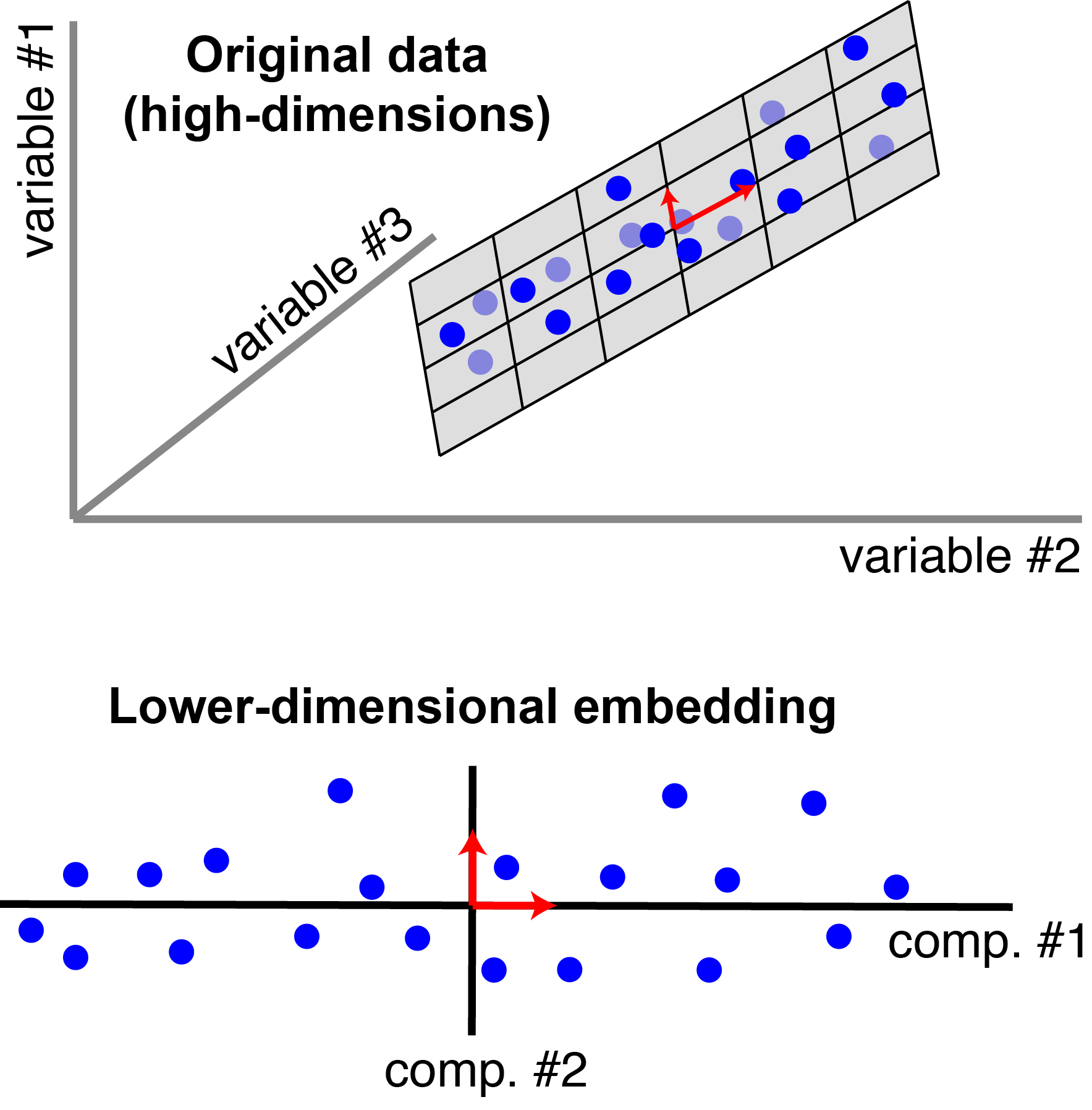
This articles focuses on the applications of PCA, hence it doesn't go into the details of why PCA works. However to understand why PCA works one can read OpenGenus IQ article: Why Principal Component Analysis (PCA) works?.
Get a deeper background on PCA:
Now that we are done with understanding what PCA is and why PCA works we can focus on the applications of PCA. The principal application of PCA is dimension reduction. If you have high dimensional data, PCA allows you to reduce the dimensionality of your data so the bulk of the variation that exists in your data across many high dimensions is captured in fewer dimensions.
PCA is used abundantly in all forms of analysis - from Neuroscience to Quantitative Finance. PCA has wide-spread applications in various industries. The most significant applications of PCA are mentioned below:
PCA is a methodology to reduce the dimensionality of a complex problem. Say, a fund manager has 200 stocks in his portfolio. To analyze these stocks quantiatively a stock manager will require a co-relational matrix of the size 200 * 200, which makes the problem very complex.
However if he was to extract, 10 Principal Components which best represent the variance in the stocks best, this would reduce the complexity of problem while still explaining the movement of all 200 stocks. Some other applications of PCA include:
PCA is also used for image compression. Below mentioned is an example of Image Compression of the OpenGenus Logo using Principal Component Analysis.
Importing the required libraries:
import matplotlib.image as mpimg import matplotlib.pyplot as plt import numpy as np from sklearn.decomposition import PCA Reading the Open Genus Logo as input:
img = mpimg.imread('opengenus_logo.png') Printing the shape of the image:
print(img.shape) #Showing the image plt.imshow(img) Output:
(156, 194, 3)
Our image is in the form of 156 rows each containing 196 pixels which have 3 channels(RGB). We have to resize the image so that it is in the format required for PCA input. As 196*3=588, we resize the image to (156,582):
img_r = np.reshape(img, (156, 582)) print(img_r.shape) Running PCA with 32 Principal Components:
pca = PCA(32).fit(img_r) img_transformed = pca.transform(img_r) print(img_transformed.shape) print(np.sum(pca.explained_variance_ratio_) ) With these 32 components we are able to express 98.7% of the variance.
Inverse transforming the PCA output and reshaping for visualization using imshow:
temp = pca.inverse_transform(img_transformed) print(temp.shape) temp = np.reshape(temp, (156, 194 ,3)) print(temp.shape) plt.imshow(temp) If we similarly compress images using 8, 16 and 64 Principle Components we are able to express the following percentages of variance of the original image:
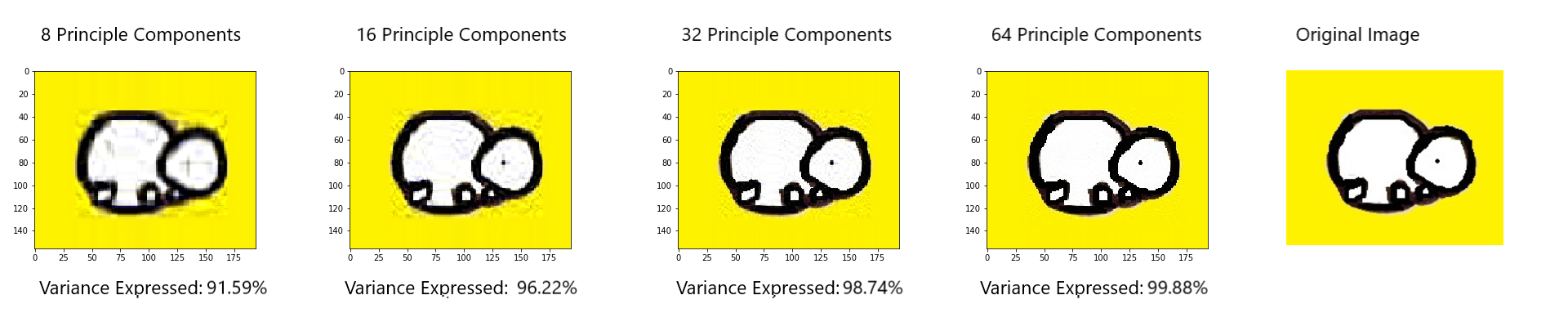
| Number of Principal Components | Percentage of Variance Expressed |
|---|---|
| 8 | 91.59% |
| 16 | 96.22% |
| 32 | 98.74% |
| 64 | 99.88% |
I highly recommend that you try to implement the above mentioned code yourself as well. The code along with the input image can be found on my Github account.
PCA has also been used in various other application which are mentioned below:

Read more posts by this author.
Improved & Reviewed by:
— OpenGenus IQ: Learn Algorithms, DL, System Design —Difflib is a module that contains several easy-to-use functions and classes that allow users to compare sets of data. The module presents the results of these sequence comparisons in a human-readable format, utilizing deltas to display the differences more cleanly.

Lyndi Castrejon
In C++, the goto statement is a jump statement used to transfer unconditional control to a specified label. In other words, it allows you to jump from any starting point to any ending point in a program, altering the program's flow.